온라인 정수열 사전

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

온라인 정수열 사전(OEIS)은 닐 슬론이 1964년 시작하여 현재까지 운영되는 정수열 데이터베이스이다. 슬론은 조합론 연구를 지원하기 위해 정수열을 수집하기 시작했으며, 1973년과 1995년에 정수열 핸드북과 백과사전을 출판했다. 이후 온라인 데이터베이스로 전환하여 현재 36만 개 이상의 수열을 포함하고 있다. OEIS는 각 수열에 고유한 ID 번호와 이름, 수열 자체, 오프셋, 코멘트, 참고 문헌, 링크, 공식, 예시, 프로그램, 상호 참조, 키워드 등의 정보를 제공한다. 키워드는 수열의 특징을 나타내며, 정수가 아닌 수와 자기 참조 수열도 다루고 있다. 슬론의 간극은 OEIS 데이터베이스에서 정수의 "중요도"를 측정하는 데 사용되는 현상이다.

더 읽어볼만한 페이지

수학 프로젝트 - 수학 계보 프로젝트
수학 계보 프로젝트는 해리 쿤스가 1997년 시작한 온라인 프로젝트로, 수학자와 관련 분야 학자들의 학문적 계보를 데이터베이스화하여 추적하며 자기 보고에 의존하지만 11세기까지 거슬러 올라가는 정보도 포함한다.
수학 프로젝트 - 밀레니엄 수학 프로젝트
밀레니엄 수학 프로젝트는 젊은 세대의 수학적 사고 능력 향상과 수학에 대한 관심 증진을 목표로 에니그마 학교 워크숍, NRICH, 체험 수학 로드쇼 등 다양한 교육 프로그램을 제공하는 프로젝트이다.
수학 데이터베이스 - 수학 리뷰
수학 리뷰는 오토 E. 노이게바우어가 나치 검열을 피하고자 1940년에 설립한 수학 학술지 및 온라인 데이터베이스로, 전 세계 수학 연구 출판물에 대한 리뷰를 제공하며 MathSciNet을 통해 1940년 이후의 자료와 수학 인용 지수를 제공하지만 평가 주관성 및 지수 방식의 한계에 대한 비판도 존재한다.
수학 데이터베이스 - 첸트랄블라트 마트
첸트랄블라트 마트는 수학, 응용 수학 및 관련 분야의 논문, 회의 논문, 서적 등에 대한 리뷰를 제공하는 서비스이며, 1931년 창간되어 zbMATH라는 이름의 온라인 서비스로 제공되다가 2021년부터 zbMATH Open이라는 이름으로 무료 데이터베이스를 운영한다.
수학 웹사이트 - 칸 아카데미
칸 아카데미는 살만 칸이 2008년에 설립한 비영리 교육 기관으로, 다양한 분야의 교육용 비디오와 연습 문제, 학습 관리 도구 등을 무료로 제공하며 숙달 학습 및 거꾸로 학습을 지원한다.
수학 웹사이트 - 울프럼 알파
울프럼 알파는 자연어 처리 기반 지식 엔진으로, 텍스트 입력을 통해 질문에 대한 답변과 복잡한 계산, 통계 분석, 금융 계산 등의 연산 결과를 제공하고 시각화한다.

온라인 정수열 사전 - [IT 관련 정보]에 관한 문서
기본 정보
이름	온라인 정수열 대사전
영어 이름	On-Line Encyclopedia of Integer Sequences
약칭	OEIS
설명	온라인 데이터베이스
분야	정수열
사용 언어	영어
항목 수 (2024년 2월 기준)	300,000 항목 이상
접속	무료
등록	선택 사항 (항목 편집 또는 새로운 항목 제출 시 필요)
라이선스	크리에이티브 커먼즈 CC BY-SA 4.0
설립	1995년
설립자	니얼 슬론
관리인	OEIS 재단 (OEIS Foundation)
운영	OEIS 재단
이전	Handbook of Integer Sequences Encyclopedia of Integer Sequences
추가 정보
목표	연구자들에게 유용한 정보 제공 정수열에 대한 정보의 중앙 저장소 역할 수학적 발견 지원
이메일 서버 및 슈퍼시커	슈퍼시커는 OEIS에 아직 없는 수열을 식별하는 데 도움을 주는 프로그램임. 사용자가 이메일을 통해 수열을 보내면 슈퍼시커가 기존 데이터베이스와 비교하여 결과를 반환함.
관련 링크
공식 웹사이트	온라인 정수열 대사전
OEIS 재단	OEIS 재단

2. 역사

닐 슬론은 1960년대 중반 조합론 연구를 위해 정수열을 수집하기 시작했다. 초기에는 천공 카드를 이용하여 데이터를 정리하였으며, 1973년과 1995년에 두 권의 책으로 출판하였다.

1994년 8월, 슬론은 온라인 정수열 사전(OEIS)의 전신인 이메일 서비스를 시작했고, 1996년에는 웹사이트를 개설했다. 이후 OEIS는 꾸준히 성장하여 2004년 10만 번째 수열이 등록되었고, 2011년 11월에는 20만 번째 수열이, 2018년 2월에는 30만 번째 수열이 추가되었다. 2023년 1월 말 기준으로 36만 개 이상의 수열이 OEIS에 포함되어 있다.

슬론은 2002년부터 부편집자 및 자원 봉사자 위원회의 도움을 받아 OEIS를 관리해왔다. 2004년에는 10만 번째 수열 추가를 기념했고, 2006년에는 사용자 인터페이스 개선 및 검색 기능이 추가되었다. 2010년에는 OEIS 위키가 만들어져 편집자와 기여자 간의 협업을 돕고 있다.

2. 1. 닐 슬론의 초기 수집 활동 (1964년 ~ 1995년)

닐 슬론은 1964년 대학원생 시절 조합론 연구를 지원하기 위해 정수열을 수집하기 시작했다.^[8]^[9] 데이터베이스는 처음에는 천공 카드에 저장되었다. 그는 데이터베이스에서 선별한 내용을 두 번 책으로 출판했다.

출판년도	제목	포함된 수열 개수	비고
1973	정수열 핸드북 (A Handbook of Integer Sequences)	2,372개	사전식 순서로 배열, 1번부터 2372번까지 번호 할당
1995	정수열 백과사전 (The Encyclopedia of Integer Sequences)	5,488개	시몬 플루프와 공동 제작, M0000부터 M5487까지 M-번호 할당, 정수열 핸드북의 수열에 대한 N-번호(N0001부터 N2372) 참조 포함

이 책들은 좋은 반응을 얻었고, 특히 두 번째 출판 이후 수학자들은 슬론에게 꾸준히 새로운 수열을 제공했다. 이 컬렉션은 책 형태로 관리하기 어려워졌고, 데이터베이스가 16,000개의 항목에 도달했을 때 슬론은 온라인으로 전환하기로 결정했다. 처음에는 이메일 서비스(1994년 8월)로 시작했고, 곧 웹사이트(1996년)로 전환했다. 데이터베이스 작업의 부수적인 결과로 슬론은 1998년 ''정수열 저널''을 창간했다.^[10]

슬론은 거의 40년 동안 '자신의' 수열을 개인적으로 관리해 왔지만, 2002년부터는 부편집자 및 자원 봉사자들로 구성된 위원회가 이 포괄적인 데이터베이스를 유지 관리하는 데 도움을 주고 있다.^[11]

2. 2. 온라인 데이터베이스 구축 (1994년 ~ 현재)

닐 슬론이 1964년 대학원생 시절 조합론 연구를 지원하기 위해 정수열을 수집하기 시작했을 때, 데이터베이스는 처음에는 천공 카드에 저장되었다.^[8]^[9] 그는 데이터베이스에서 선별한 내용을 두 번 책으로 출판했다.

출판 년도	제목	포함된 수열 개수	비고
1973	정수열 핸드북 (A Handbook of Integer Sequences)	2,372개	사전식 순서로 배열, 1번부터 2372번까지 번호 할당
1995	정수열 백과사전 (The Encyclopedia of Integer Sequences)	5,488개	시몬 플루프와 공동 제작, M0000부터 M5487까지 M-번호 할당, 정수열 핸드북의 수열 참조 포함 (N-번호, 초기 용어 차이 있을 수 있음)

이 책들은 좋은 반응을 얻었고, 특히 두 번째 출판 이후 수학자들은 슬론에게 꾸준히 새로운 수열을 제공했다. 컬렉션이 책 형태로 관리하기 어려워져, 슬론은 데이터베이스가 16,000개에 도달했을 때 온라인으로 전환하기로 결정했다. 1994년 8월 이메일 서비스를 시작했고, 곧 1996년 웹사이트로 전환했다. 데이터베이스 작업의 부수적인 결과로 슬론은 1998년 ''정수열 저널''을 창간했다.^[10]

데이터베이스는 연간 약 10,000개의 항목의 속도로 계속 증가하고 있다. 슬론은 거의 40년 동안 '자신의' 수열을 개인적으로 관리해 왔지만, 2002년부터는 부편집자 및 자원 봉사자들로 구성된 위원회가 데이터베이스를 유지 관리하는 데 도움을 주고 있다.^[11] 2004년, 슬론은 이샹고 뼈의 표시를 세는 수열을 데이터베이스에 10만 번째 수열로 추가한 것을 기념했다. 2006년에는 사용자 인터페이스가 개선되었고 더 발전된 검색 기능이 추가되었다. 2010년에는 OEIS 편집자와 기여자의 협업을 단순화하기 위해 [//oeis.org/wiki/ OEIS 위키]가 [//oeis.org/ OEIS.org]에 생성되었다.^[12] 20만 번째 수열은 2011년 11월에 데이터베이스에 추가되었다. 2018년 2월에는 30만번째 수열이 정의되었으며, 2023년 1월 말까지 데이터베이스에는 36만 개 이상의 수열이 포함되어 있었다.^[16]^[17]

3. OEIS의 구성 및 용어

OEIS는 사전식 순서를 유지하며, 각 수열은 선행 수열과 후행 수열("맥락")을 갖는다.^[18] 정규화를 위해 (일반적으로) 초기 0과 1, 각 요소의 부호를 무시한다. 가중치 분포 코드의 수열은 주기적으로 반복되는 0을 생략하는 경우가 많다.

예를 들어, 소수, 팰린드롬 소수, 피보나치 수열, 게으른 요리사 수열, $\textstyle$ 의 급수 전개에서의 계수는 OEIS 사전식 순서에서 다음과 같다.

수열 #1 (A000040): 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...
수열 #2 (A002385): 2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, ...
수열 #3 (A000045): 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, ...
수열 #4 (A000124): 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, 67, 79, 92, 106, 121, 137, 154, ...
수열 #5 (A046970): -3, -8, -3, -24, 24, -48, -3, -8, 72, -120, 24, -168, 144, ...

정규화되지 않은 사전식 순서는 이러한 수열을 #3, #5, #4, #1, #2 순서로 정렬한다.

OEIS의 주요 구성 요소와 용어는 다음과 같다.

ID 번호: 각 수열에 부여된 고유한 식별자로, 'A'와 6자리 숫자로 구성된다. (예: A000040)
이름: 수열의 일반적인 이름과 공식(있는 경우)을 포함한다.
수열 데이터: 약 260자 정도의 숫자 목록을 제공한다. 더 많은 항은 B-파일에서 제공될 수 있다.^[22]
오프셋: 주어진 첫 번째 항의 인덱스를 나타낸다.
코멘트: 다른 필드에 적합하지 않은 수열 관련 정보를 제공한다.
참조: 인쇄된 문서(책, 논문 등)에 대한 참조를 제공한다.
링크: 온라인 리소스(관련 기사, 텍스트 파일, 이미지 등)에 대한 URL 링크를 제공한다.
공식: 수열에 대한 공식, 점화식, 생성 함수 등을 제공한다.
예시: 수열 멤버 값의 몇 가지 예를 제공한다.
프로그래밍 코드: Maple, 매스매티카 등 다양한 프로그래밍 언어로 작성된 코드를 제공한다.
상호 참조: 다른 수열과의 관계를 나타낸다.
키워드: 수열을 분류하는 4글자 키워드를 제공한다. (예: base, cofr, cons, core, easy, hard, sign 등)
작성자: 수열 제출자의 이름과 제출 날짜(2011년 이전 제출의 경우 이메일 주소 포함)를 제공한다.
확장: 수열을 확장하거나 수정한 사람의 이름과 날짜를 제공한다.

3. 1. ID 번호 (식별 번호)

OEIS의 모든 수열은 'A'로 시작하는 6자리 양의 정수인 일련 번호를 가지며(2004년 11월 이전에는 왼쪽을 0으로 채움), 'A'는 "절대"를 의미한다.^[18] 번호는 편집자 또는 A 번호 분배자에 의해 할당되는데, 이는 기여자가 한 번에 여러 개의 관련 수열을 보내고 상호 참조를 만들 수 있도록 할 때 유용하다. 분배자로부터 받은 A 번호는 사용하지 않으면 발행 후 한 달 후에 만료된다.

수열	설명	날짜
	이항 계수 C(2n, n)이 홀수 소수의 제곱으로 나누어 떨어지지 않음을 만족하는 숫자 n.
	피보나치(n)!.
	정확히 24의 차수를 갖는 대칭군을 가진 n개의 셀을 가진 3차원 폴리오미노 (또는 폴리큐브)의 수.
	n · a(n)이 n개의 연속적인 정수의 연결인 가장 작은 수.
	ζ(3/2)에 대한 연분수.
	−k ≤ p(i) − i ≤ r 및 p(i) − i를 만족하는 순열의 수.
	n번째 소수의 이진 전개에서 1의 가장 긴 연속 블록의 길이.
	A069321(0) = 0으로 설정한 A069321(n)의 자체에 대한 지수 컨볼루션.
	콩고에서 온 22,000년 된 이샹고 뼈에서 온 표시.
	삼각형 A102230의 열 1, A032349와 A032349 오른쪽 시프트의 컨볼루션과 같습니다.
	니븐 수의 합이 필요한 n부터 시작하는 연속 정수의 수.
	삼각형이 없는 양의 정수.
	곱셈을 고려한 n의 소수 약수의 합의 뫼비우스 변환.

OEIS의 이전 책에 있는 수열의 ID 번호는 동일하지 않다. 1973년의 ''정수 수열 핸드북''에는 약 2400개의 수열이 포함되어 있었으며, 사전식 순서(문자 N과 4자리 숫자, 필요한 경우 0으로 채움)로 번호가 매겨졌다. 1995년의 ''정수 수열 백과사전''에는 5487개의 수열이 포함되어 있었으며, 역시 사전식 순서(문자 M과 4자리 숫자, 필요한 경우 0으로 채움)로 번호가 매겨졌다. 이러한 이전 M 및 N 번호는 해당되는 경우 현대 A 번호 뒤 괄호 안에 ID 번호 필드에 포함되어 있다.

데이터베이스에 등록된 모든 수열에는 6자리의 식별 번호(ID number)가 할당되어 있으며, 앞에 A를 붙여 표시한다. 'A000796' 대신 'A796'을 사용하는 등, 종종 앞의 0은 생략된다.

OEIS에 등록된 모든 수열에 할당된 6자리 식별 번호로, 앞에 A를 붙여 표시한다. 논문, 책, 외부 사이트에서 수열을 나타내기 위해 "OEIS의 A(A in OEIS)" 또는 단순히 "슬론의 A(Sloane's A)"와 같이 표기될 정도로 널리 알려져 있다.

이전에는 현재와는 다른 식별 번호가 사용되었다. 1973년 출판된 ''정수 수열 핸드북''(Handbook of Integer Sequences)에서는 약 2400개의 수열이 사전식 순서로 나열되었고, M이 붙은 4자리 식별 번호가 부여되었다. 1995년 출판된 ''정수 수열 백과사전''(Encyclopedia of Integer Sequences)에서는 5487개의 수열이 역시 사전식 순서로 나열되었고, N이 붙은 4자리 식별 번호가 부여되었다. 이러한 이전 식별 번호는 A가 붙은 새로운 식별 번호와 마찬가지로 사용할 수 있으며, 이 항목에 기재되어 있다.

3. 2. 이름 (Name)

닐 슬론이 1964년 대학원생 시절 조합론 연구를 지원하기 위해 정수열을 수집하기 시작하면서, 이 사전의 역사가 시작되었다.^[8]^[9] 초기에는 천공 카드에 저장되었던 데이터베이스는, 슬론에 의해 두 권의 책으로 출판되었다.

# '''''정수열 핸드북''''' (1973년): 사전식 순서로 2,372개의 수열을 포함하고 있으며, 1번부터 2372번까지 번호가 할당되었다.

# '''''정수열 백과사전''''' (1995년): 시몬 플루프와 함께 제작되었으며, 5,488개의 수열을 포함하고 M0000부터 M5487까지 M-번호가 할당되었다. 이 백과사전에는 ''정수열 핸드북''의 해당 수열에 대한 참조가 N-번호(N0001부터 N2372)로 표시되어 있다.

이 책들은 좋은 반응을 얻었고, 수학자들로부터 새로운 수열을 꾸준히 제공받게 되면서 슬론은 온라인화를 결정했다. 1994년 이메일 서비스로 시작하여 1996년 웹사이트로 전환하면서, 온라인 정수열 사전, 즉 OEIS가 탄생하게 되었다.

3. 3. 수열 (Sequence)

닐 슬론(Neil Sloane)이 조합론 연구를 지원하기 위해 1964년부터 정수열을 수집하기 시작했다.^[8]^[9] 초기에는 천공 카드에 저장되었던 데이터베이스는, 선별된 내용이 두 권의 책으로 출판되었다.

'''정수열 핸드북'''(1973): 사전식 순서로 2,372개의 수열을 포함하며, 1번부터 2372번까지 번호가 할당되었다.
'''정수열 백과사전''' (1995): 시몬 플루프(Simon Plouffe)와 함께 제작되었으며, 5,488개의 수열을 포함하고 M0000부터 M5487까지 M-번호가 할당되었다. ''정수열 핸드북''의 수열은 N0001부터 N2372로 참조되었다.

이 책들은 좋은 반응을 얻었고, 수학자들은 슬론에게 꾸준히 새로운 수열을 제공했다. 컬렉션이 책 형태로 관리하기 어려워지고 16,000개 항목에 도달하자, 슬론은 온라인 전환을 결정했다. 1994년 이메일 서비스로 시작하여 1996년 웹사이트로 전환되었다. 슬론은 1998년 ''정수열 저널''을 창간했다.^[10]

데이터베이스는 연간 약 10,000개 항목의 속도로 계속 증가했다. 슬론은 거의 40년 동안 '자신의' 수열을 개인적으로 관리했지만, 2002년부터 부편집자 및 자원 봉사자 위원회가 데이터베이스 유지 관리를 돕고 있다.^[11] 2004년, 슬론은 이샹고 뼈의 표시를 세는 수열을 10만 번째 수열로 추가했다. 2006년에는 사용자 인터페이스가 개선되고 더 발전된 검색 기능이 추가되었다. 2010년에는 OEIS 편집자와 기여자의 협업을 단순화하기 위해 [//oeis.org/wiki/ OEIS 위키]가 생성되었다.^[12] 20만 번째 수열은 2011년 11월에 추가되었다.^[13]^[14]^[15] A300000은 2018년 2월에 정의되었으며, 2023년 1월 말까지 데이터베이스에는 36만 개 이상의 수열이 있었다.^[16]^[17]

OEIS는 수열의 사전식 순서를 유지하며, 각 수열은 선행 수열과 후행 수열("맥락")을 갖는다.^[18] 정규화를 위해 초기 0과 1, 각 요소의 부호를 무시한다. 가중치 분포 코드의 수열은 주기적으로 반복되는 0을 생략하는 경우가 많다.

예를 들어, 소수, 팰린드롬 소수, 피보나치 수열, 게으른 요리사 수열,

\textstyle

의 급수 전개 계수는 OEIS 사전식 순서에서 다음과 같다.

수열 #1: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...
수열 #2: 2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, ...
수열 #3: 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, ...
수열 #4: 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, 67, 79, 92, 106, 121, 137, 154, ...
수열 #5: 3, 8, 3, 24, 24, 48, 3, 8, 72, 120, 24, 168, 144, ...

정규화되지 않은 사전식 순서는 #3, #5, #4, #1, #2 순서로 정렬된다.

0은 종종 존재하지 않는 수열 요소를 나타내는 데 사용된다. 예를 들어, "최소 소수 ''n''²개의 연속된 소수를 사용하여 최소 마법 상수의 ''n'' × ''n'' 마방진을 만들거나, 그러한 마방진이 존재하지 않으면 0"을 열거한다. ''a''(1)은 2, ''a''(3)는 1480028129지만, 2 × 2 마방진은 존재하지 않으므로 ''a''(2)는 0이다. 오일러 피 함수 값 함수 ''N''_φ(''m'')는 φ(''x'') = ''m''의 해의 수를 계산하는데, 4에 대한 해는 4개지만 14에 대한 해는 없어 ''a''(14)는 0이다.

다른 값도 사용되며, 가장 흔하게는 −1이 사용된다.

OEIS의 모든 수열은 A로 시작하는 6자리 양의 정수인 일련 번호를 가지며, A는 "절대"를 의미한다. 번호는 편집자 또는 A 번호 분배자에 의해 할당된다. 다음은 임의로 선택된 수열의 예이다.

수열	설명	생성일
	이항 계수 C(2n, n)이 홀수 소수의 제곱으로 나누어 떨어지지 않음을 만족하는 숫자 n.	2001년 1월 1일
	피보나치(n)!.	2001년 3월 14일
	정확히 24의 차수를 갖는 대칭군을 가진 n개의 셀을 가진 3차원 폴리오미노 (또는 폴리큐브)의 수.	2002년 1월 1일
	n · a(n)이 n개의 연속적인 정수의 연결인 가장 작은 수 ...	2002년 8월 31일
	ζ(3/2)에 대한 연분수	2003년 1월 1일
	−k ≤ p(i) − i ≤ r 및 p(i) − i를 만족하는 순열의 수	2003년 2월 10일
	n번째 소수의 이진 전개에서 1의 가장 긴 연속 블록의 길이.	2003년 11월 20일
	A069321(0) = 0으로 설정한 A069321(n)의 자체에 대한 지수 컨볼루션.	2004년 1월 1일
	콩고에서 온 22,000년 된 이샹고 뼈에서 온 표시.	2004년 11월 7일
	삼각형 A102230의 열 1, A032349와 A032349 오른쪽 시프트의 컨볼루션과 같습니다.	2005년 1월 1일
	니븐 수의 합이 필요한 n부터 시작하는 연속 정수의 수.	2005년 7월 8일
	삼각형이 없는 양의 정수.	2006년 1월 12일
	곱셈을 고려한 n의 소수 약수의 합의 뫼비우스 변환.	2006년 6월 2일

3. 4. 오프셋 (Offset)

OEIS의 각 수열에는 A로 시작하는 6자리 양의 정수인 일련 번호가 할당된다. 이 번호는 '절대적'이라는 의미를 가진다. 번호는 편집자나 A 번호 분배자에 의해 할당되며, 기여자가 여러 관련 수열을 보내고 상호 참조를 만들 수 있도록 돕는다. 분배자로부터 받은 A 번호는 사용하지 않으면 발행 후 한 달 후에 만료된다.

OEIS의 이전 책에 있는 수열의 ID 번호는 동일하지 않다. 1973년의 ''정수 수열 핸드북''에는 약 2400개의 수열이 사전식 순서(문자 N과 4자리 숫자)로 번호가 매겨졌고, 1995년의 ''정수 수열 백과사전''에는 5487개의 수열이 사전식 순서(문자 M과 4자리 숫자)로 번호가 매겨졌다. 이러한 이전 M 및 N 번호는 해당하는 경우 현대 A 번호 뒤 괄호 안에 ID 번호 필드에 포함되어 있다.
오프셋은 주어진 첫 번째 항의 색인을 의미한다. 즉, 오프셋이 n이면 첫째 항은 a(n)으로 표기한다. 예를 들어, 제곱수 수열 a(n) = n²을 0, 1, 4, 9, 16, 25, ...로 나열하면 오프셋은 0이지만, 1, 4, 9, 16, 25, ...로 시작한다면 오프셋은 1이다. 대부분의 수열의 오프셋은 0 또는 1이다.

A073502 : 오프셋이 3인 수열의 예. 첫째 항 a(3)은 가능한 작은 소수와 1을 사용하여 3 × 3의 마방진을 만들었을 때, 각 행의 합이다.
A072171 : 오프셋이 -1인 수열의 예. 첫째 항 a(-1)은 -1등성, 즉 겉보기 등급이 -1.5에서 -0.5까지의 항성의 개수이다.

때로는 첫째 항에 채용해야 할 항에 대해 의견이 갈리는 경우가 있다. 예를 들어, 레이지 케이터러 수열(A000124)의 경우, OEIS는 1, 2, 4, 7, 11, 16, 22, 29, 37, ... (오프셋 0)으로 시작하는 반면, Mathworld는 2, 4, 7, 11, 16, 22, 29, 37, ... (오프셋 1)로 시작한다.

오프셋 란에는 일반적으로 두 개의 숫자가 기재되어 있다. 첫 번째 숫자는 위에 설명된 의미를 가지며, 두 번째 숫자는 "절대값이 1보다 큰 수가 처음 나타나는 것은 첫째 항부터 세어 몇 번째 항인가"를 나타낸다. 이 두 번째 숫자는 검색 속도를 높이는 데 도움이 된다. 예를 들어, A000001은 1, 1, 1, 2로 시작하며, 오프셋 란에는 '''0, 5'''라고 기재되어 있다.

3. 5. 코멘트 (Comment)

닐 슬론(Neil Sloane)은 1964년 대학원생 시절 조합론 연구를 돕기 위해 정수열을 수집하기 시작했다.^[8]^[9] 처음에는 천공 카드에 저장되었던 이 데이터베이스는, 선별된 내용이 두 번의 책으로 출판되었다.

# '''''정수열 핸드북'''''(1973): 사전식 순서로 2,372개의 수열을 포함하며, 1번부터 2372번까지 번호가 할당되었다.

# '''''정수열 백과사전''''' (1995): 시몬 플루프(Simon Plouffe)와 함께 제작, 5,488개의 수열을 포함하며, M0000부터 M5487까지 M-번호가 할당되었다. ''정수열 핸드북''의 해당 수열에 대한 참조(N0001부터 N2372까지 N-번호로 표시)를 포함한다.

이 책들은 좋은 반응을 얻었고, 특히 두 번째 출판 이후 수학자들은 슬론에게 꾸준히 새로운 수열을 제공했다. 16,000개의 항목에 도달했을 때, 슬론은 온라인(1994년 이메일 서비스, 1996년 웹사이트)으로 전환했다. 1998년에는 ''정수열 저널''이 창간되었다.^[10]

데이터베이스는 연간 약 10,000개 항목의 속도로 증가했다. 슬론은 거의 40년 동안 '자신의' 수열을 관리했지만, 2002년부터 부편집자 및 자원 봉사자 위원회가 데이터베이스 유지를 돕고 있다.^[11]

2004년, 슬론은 이샹고 뼈의 표시를 세는 A100000번 수열을 10만 번째 수열로 추가했다. 2006년에는 사용자 인터페이스가 개선되고 더 발전된 검색 기능이 추가되었다. 2010년에는 OEIS 편집자와 기여자의 협업을 단순화하기 위해 [//oeis.org/wiki/ OEIS 위키]가 생성되었다.^[12] 20만 번째 수열인 A200000은 2011년 11월에 추가되었다.^[13]^[14]^[15] A300000은 2018년 2월에 정의되었으며, 2023년 1월 말까지 데이터베이스에는 36만 개 이상의 수열이 포함되어 있었다.^[16]^[17]

3. 6. 참고 문헌 (References)

영어 위키백과 OEIS 수열 목록을 보려면 List of OEIS sequences|OEIS 수열 목록^영어을 참조하라.
한국어 위키백과에 등록된 OEIS 수열 목록을 보려면 특수:가리키는문서/틀:OEIS, 특수:가리키는문서/틀:OEIS2C를 참조하라.
10만개 이상의 수열표
N. J. A. Sloane, "My favorite integer sequences", in Sequences and their Applications (Proceedings of SETA '98), C. Ding, T. Helleseth, and H. Niederreiter, eds., Springer-Verlag, London, 1999, pp. 103–130.
N. J. A. Sloane, "The On-Line Encyclopedia of Integer Sequences", Notices of the American Mathematical Society, vol. 50, no. 8, 2003, pp. 912–915.
N. J. A. Sloane and S. Plouffe, ''The Encyclopedia of Integer Sequences'', Academic Press, San Diego, 1995.
Sara C. Billey and Bridget E. Tenner, "Fingerprint databases for theorems", Notices of the American Mathematical Society, vol. 60, no. 8, 2013, pp. 1034–1039.

닐 슬론(Neil Sloane)은 1964년 대학원생 시절 조합론 연구를 지원하기 위해 정수열을 수집하기 시작했다.^[8]^[9]

'''''정수열 핸드북'''''(1973)
'''''정수열 백과사전''''' (1995)

슬론은 1998년 ''정수열 저널''을 창간했다.^[10]

2004년, 슬론은 이샹고 뼈의 표시를 세는 A100000번 수열을 데이터베이스에 10만 번째 수열로 추가했다. 2010년에는 OEIS 편집자와 기여자의 협업을 단순화하기 위해 [//oeis.org/wiki/ OEIS 위키]가 [//oeis.org/ OEIS.org]에 생성되었다.^[12] 20만 번째 수열인 A200000은 2011년 11월에 데이터베이스에 추가되었다.^[13]^[14]^[15] A300000은 2018년 2월에 정의되었으며, 2023년 1월 말까지 데이터베이스에는 36만 개 이상의 수열이 포함되어 있었다.^[16]^[17]

M. Abramowitz 및 I. A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, pp. 805-811.
T. M. Apostol, Introduction to Analytic Number Theory, Springer-Verlag, 1986, p. 48.
Reinhard Zumkeller, n = 1..10000에 대한 n, a(n) 테이블
M. Abramowitz 및 I. A. Stegun, eds., Handbook of Mathematical Functions, National Bureau of Standards, Applied Math. Series 55, Tenth Printing, 1972 [대체 스캔 사본].
P. G. Brown, Some comments on inverse arithmetic functions, Math. Gaz. 89 (516) (2005) 403-408.
Paul W. Oxby, A Function Based on Chebyshev Polynomials as an Alternative to the Sinc Function in FIR Filter Design, arXiv:2011.10546 [eess.SP], 2020.
Wikipedia, 리만 제타 함수.

3. 7. 링크 (Links)

OEIS 재단 홈페이지(https://oeisf.org/)
OEIS 위키(https://oeis.org/wiki/Welcome)
[http://www.jjj.de/fxt/#fxtbook 4차 다항식의 근의 공식] (Jörg Arndt|요르그 아른트^de 작성)
Hmmm... Integer Sequences|흠... 정수 수열^영어 (Mike Gerome|마이크 제롬^영어 작성)
[http://www.math.uwaterloo.ca/tsp/index.html 정수 수열 변환] (David Applegate|데이비드 앱클게이트^영어, Marc LeBrun|마크 르브런^영어, Neil Sloane|닐 슬론^영어 작성)
[http://www.cecm.sfu.ca/projects/ISC.html 역 심볼 계산기] (Boris Zimmermann|보리스 짐머만^영어, Simon Plouffe|사이먼 플루프^영어 작성)
[http://www.wayback.archive.org/web/20100202042811/http://www.research.att.com/~njas/sequences/transforms.html 정수 수열 변환] (Neil Sloane|닐 슬론^영어 작성)
[http://www.wayback.archive.org/web/20070714000621/http://www.research.att.com/~njas/sequences/ol.html 정수 수열의 오래된 목록] (Neil Sloane|닐 슬론^영어 작성)
[http://www.wayback.archive.org/web/20100619025451/http://www.research.att.com/~njas/sequences/sloa0000.txt 슬론의 A000000 파일] (Neil Sloane|닐 슬론^영어 작성)
[http://www.wayback.archive.org/web/20100127095136/http://www.research.att.com/~njas/sequences/notes.dvi 슬론의 수열 노트] (Neil Sloane|닐 슬론^영어 작성)
The Puzzlers|수열 퍼즐러^영어 (Carlos Rivera|카를로스 리베라^영어 작성)
[https://web.archive.org/web/20170703182833/http://www.primepuzzles.net/puzzles/puzz_236.htm 수열 퍼즐 236 - 2003년의 OEIS] (Carlos Rivera|카를로스 리베라^영어 작성)
[http://www.wayback.archive.org/web/20090303013033/http://www.research.att.com/~njas/sequences/zagier.html 돈 재기어(Don Zagier)가 선택한 좋아하는 세 개의 수열] (Neil Sloane|닐 슬론^영어 작성)

3. 8. 공식 (Formula)

닐 슬론(Neil Sloane)이 1973년에 출간한 '''''정수열 핸드북'''''(A Handbook of Integer Sequences^영어)에는 사전식 순서로 정렬된 2,372개의 수열이 포함되어 있으며, 각 수열에는 1부터 2372까지의 번호가 할당되었다.^[8]^[9] 1995년에 슬론은 시몬 플루프(Simon Plouffe)와 함께 '''''정수열 백과사전'''''(The Encyclopedia of Integer Sequences^영어)을 출간했는데, 여기에는 5,488개의 수열이 M0000부터 M5487까지의 M-번호와 함께 수록되었다. 이 백과사전에는 ''정수열 핸드북''에 있는 해당 수열에 대한 N-번호(N0001부터 N2372까지) 참조도 포함되어 있다.^[8]^[9]

다음은 주어진 문서 A046970에 대한 공식의 예시이다.

a(p^e) = 1 - p^2인 곱셈.
a(n) = Sum_{d|n} mu(d)*d^2.
abs(a(n)) = Product_{p prime divides n} (p^2 - 1). - Jon Perry, 2010년 8월 24일
Wolfdieter Lang, 2011년 6월 16일:
디리클레 생성 함수: zeta(s)/zeta(s-2).
a(n) = J_{-2}(n)*n^2, with the Jordan function J_k(n), with J_k(1):=1. Apostol 참고 자료, p. 48. 연습문제 17.
a(prime(n)) = -A084920(n). - R. J. Mathar, 2011년 8월 28일
G.f.: Sum_{k>=1} mu(k)*k^2*x^k/(1 - x^k). - Ilya Gutkovskiy, 2017년 1월 15일

3. 9. 예시 (Example)

닐 슬론(Neil Sloane)이 1964년 대학원생 시절 조합론 연구를 돕기 위해 정수열을 수집하기 시작한 이후, 10만 개 이상의 수열이 이 데이터베이스에 포함되었다.^[8]^[9] 슬론은 처음에 천공 카드에 데이터를 저장했고, 나중에 두 권의 책으로 출판했다.

'''정수열 핸드북'''''(1973): 사전식 순서로 2,372개의 수열을 포함하며, 1번부터 2372번까지 번호가 할당되었다.
'''정수열 백과사전''''' (1995): 시몬 플루프(Simon Plouffe)와 함께 제작되었으며, 5,488개의 수열을 포함하고 있으며, M0000부터 M5487까지 M-번호가 할당되었다. ''정수열 핸드북''의 수열에 대한 참조도 포함되어 있다.

이 책들은 좋은 반응을 얻었고, 특히 두 번째 출판 이후 수학자들은 슬론에게 새로운 수열을 꾸준히 제공했다. 1994년 8월에는 이메일 서비스를 시작했고, 1996년에는 웹사이트로 전환했다. 1998년에는 ''정수열 저널''을 창간했다.^[10]

데이터베이스는 연간 약 10,000개 항목의 속도로 계속 증가하고 있다. 2002년부터는 부편집자 및 자원 봉사자 위원회가 유지 관리를 돕고 있다.^[11] 2004년에는 10만 번째 수열(A100000)로 이샹고 뼈의 표시를 세는 수열이 추가되었다. 2010년에는 [//oeis.org/wiki/ OEIS 위키]가 생성되어 편집자와 기여자 간 협업을 단순화했다.^[12] 2011년 11월에는 20만 번째 수열(A200000)이 추가되었다.^[13]^[14]^[15] 2023년 1월 말까지 36만 개 이상의 수열이 포함되었다.^[16]^[17]

다음은 OEIS의 모든 필드를 포괄적으로 포함하는 예시 항목(A046970)이다.^[20]

A046970: 요르단 함수 J_2 (A007434)의 디리클레 역수.
수열: 1, -3, -8, -3, -24, 24, -48, -3, -8, 72, -120, 24, -168, 144, 192, -3, -288, 24, -360, 72, 384, 360, -528, 24, -24, 504, -8, 144, -840, -576, -960, -3, 960, 864, 1152, 24, -1368, 1080, 1344, 72, -1680, -1152, -1848, 360, 192, 1584, -2208, 24, -48, 72, 2304, 504, -2808, 24, 2880, 144, 2880, 2520, -3480, -576
OFFSET: 1, 2
COMMENTS:
B(n+2) = -B(n)*((n+2)*(n+1)/(4*Pi^2))*z(n+2)/z(n) = -B(n)*((n+2)*(n+1)/(4*Pi^2)) * Sum_{j>=1} a(j)/j^(n+2).
부호 외에는 Sum_{d|n} core(d)^2*mu(n/d) (여기서 core(x)는 x의 제곱이 아닌 부분). - Benoit Cloitre, 2002년 5월 31일
REFERENCES:
M. Abramowitz 및 I. A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, pp. 805-811.
T. M. Apostol, Introduction to Analytic Number Theory, Springer-Verlag, 1986, p. 48.
LINKS:
Reinhard Zumkeller, n = 1..10000에 대한 n, a(n) 테이블
M. Abramowitz 및 I. A. Stegun, eds., Handbook of Mathematical Functions, National Bureau of Standards, Applied Math. Series 55, Tenth Printing, 1972 [대체 스캔 사본].
P. G. Brown, Some comments on inverse arithmetic functions, Math. Gaz. 89 (516) (2005) 403-408.
Paul W. Oxby, A Function Based on Chebyshev Polynomials as an Alternative to the Sinc Function in FIR Filter Design, arXiv:2011.10546 [eess.SP], 2020.
Wikipedia, 리만 제타 함수.
FORMULA:
a(p^e) = 1 - p^2인 곱셈.
a(n) = Sum_{d|n} mu(d)*d^2.
abs(a(n)) = Product_{p prime divides n} (p^2 - 1). - Jon Perry, 2010년 8월 24일
Wolfdieter Lang, 2011년 6월 16일:
디리클레 생성 함수: zeta(s)/zeta(s-2).
a(n) = J_{-2}(n)*n^2, with the Jordan function J_k(n), with J_k(1):=1. Apostol 참고 자료, p. 48. 연습문제 17.
a(prime(n)) = -A084920(n). - R. J. Mathar, 2011년 8월 28일
G.f.: Sum_{k>=1} mu(k)*k^2*x^k/(1 - x^k). - Ilya Gutkovskiy, 2017년 1월 15일
EXAMPLE:
a(3) = -8, 3의 약수는 {1, 3}이고 mu(1)*1^2 + mu(3)*3^2 = -8이기 때문입니다.
a(4) = -3, 4의 약수는 {1, 2, 4}이고 mu(1)*1^2 + mu(2)*2^2 + mu(4)*4^2 = -3이기 때문입니다.
예를 들어, a(15) = (3^2 - 1) * (5^2 - 1) = 8*24 = 192. - Jon Perry, 2010년 8월 24일
G.f. = x - 3*x^2 - 8*x^3 - 3*x^4 - 24*x^5 + 24*x^6 - 48*x^7 - 3*x^8 - 8*x^9 + ...
MAPLE: Jinvk := proc(n, k) local a, f, p ; a := 1 ; for f in ifactors(n)[2] do p := op(1, f) ; a := a*(1-p^k) ; end do: a ; end proc: A046970 := proc(n) Jinvk(n, 2) ; end proc: # R. J. Mathar, 2011년 7월 4일
MATHEMATICA: muDD[d_] := MoebiusMu[d]*d^2; Table[Plus @@ muDD[Divisors[n]], {n, 60}] (Lopez) Flatten[Table[{ x = FactorInteger[n]; p = 1; For[i = 1, i <= Length[x], i++, p = p*(1 - xi1^2)]; p}, {n, 1, 50, 1}]] (* Jon Perry, 2010년 8월 24일 *) a[ n_] := If[ n < 1, 0, Sum[ d^2 MoebiusMu[ d], {d, Divisors @ n}]] (* Michael Somos, 2014년 1월 11일 *) a[ n_] := If[ n < 2, Boole[ n == 1], Times @@ (1 - #1^2 & /@ FactorInteger @ n)] (* Michael Somos, 2014년 1월 11일 *)
PROG:
(PARI) A046970(n)=sumdiv(n, d, d^2*moebius(d)) \\ Benoit Cloitre
(Haskell) a046970 = product . map ((1 -) . (^ 2)) . a027748_row -- Reinhard Zumkeller, 2012년 1월 19일
(PARI) {a(n) = if( n<1, 0, direuler( p=2, n, (1 - X*p^2) / (1 - X))[n])} /* Michael Somos, 2014년 1월 11일 */
CROSSREFS: 참조. A007434, A027641, A027642, A063453, A023900. 참조. A027748. 컨텍스트 시퀀스: A144457 A220138 A146975 * A322360 A058936 A280369 인접 시퀀스: A046967 A046968 A046969 * A046971 A046972 A046973
KEYWORD: sign, easy, mult
AUTHOR: Douglas Stoll, dougstoll(AT)email.msn.com
EXTENSIONS: Vladeta Jovovic, 2001년 7월 25일 수정 및 확장 Wilfredo Lopez (chakotay147138274(AT)yahoo.com)의 추가 의견, 2005년 7월 01일

OEIS의 모든 수열에는 A로 시작하는 6자리 양의 정수인 일련 번호가 할당된다. 다음은 임의로 선택된 수열의 예시이다.

수열 번호	설명	등록 날짜
	이항 계수 C(2n, n)이 홀수 소수의 제곱으로 나누어 떨어지지 않음을 만족하는 숫자 n.	2001년 1월 1일
	피보나치(n)!.	2001년 3월 14일
	정확히 24의 차수를 갖는 대칭군을 가진 n개의 셀을 가진 3차원 폴리오미노 (또는 폴리큐브)의 수.	2002년 1월 1일
	n · a(n)이 n개의 연속적인 정수의 연결인 가장 작은 수 ...	2002년 8월 31일
	ζ(3/2)에 대한 연분수.	2003년 1월 1일
	−k ≤ p(i) − i ≤ r 및 p(i) − i를 만족하는 순열의 수.	2003년 2월 10일
	n번째 소수의 이진 전개에서 1의 가장 긴 연속 블록의 길이.	2003년 11월 20일
	A069321(0) = 0으로 설정한 A069321(n)의 자체에 대한 지수 컨볼루션.	2004년 1월 1일
	콩고에서 온 22,000년 된 이샹고 뼈에서 온 표시.	2004년 11월 7일
	삼각형 A102230의 열 1, A032349와 A032349 오른쪽 시프트의 컨볼루션과 같습니다.	2005년 1월 1일
	니븐 수의 합이 필요한 n부터 시작하는 연속 정수의 수.	2005년 7월 8일
	삼각형이 없는 양의 정수.	2006년 1월 12일
	곱셈을 고려한 n의 소수 약수의 합의 뫼비우스 변환.	2006년 6월 2일

3. 10. 프로그램 (Maple, Mathematica, Program)

maple

A046970 := proc(n) Jinvk(n, 2) ; end proc: # R. J. Mathar, 2011년 7월 4일

```

```mathematica

muDD[d_] := MoebiusMu[d]*d^2; Table[Plus @@ muDD[Divisors[n]], {n, 60}] (* Lopez *)

Flatten[Table[{ x = FactorInteger[n]; p = 1; For[i = 1, i <= Length[x], i++, p = p*(1 - xi1^2)]; p}, {n, 1, 50, 1}]] (* Jon Perry, 2010년 8월 24일 *)

a[ n_] := If[ n < 1, 0, Sum[ d^2 MoebiusMu[ d], {d, Divisors @ n}]] (* Michael Somos, 2014년 1월 11일 *)

a[ n_] := If[ n < 2, Boole[ n == 1], Times @@ (1 - #1^2 & /@ FactorInteger @ n)] (* Michael Somos, 2014년 1월 11일 *)

```

```pari

(PARI) A046970(n)=sumdiv(n, d, d^2*moebius(d)) \\ Benoit Cloitre

(Haskell)

a046970 = product . map ((1 -) . (^ 2)) . a027748_row

- Reinhard Zumkeller, 2012년 1월 19일

(PARI) {a(n) = if( n<1, 0, direuler( p=2, n, (1 - X*p^2) / (1 - X))[n])} /* Michael Somos, 2014년 1월 11일 */

```

메이플과 매스매티카는 OEIS에서 수열을 계산하는 데 선호되는 프로그램이었으며, 각각 고유한 필드 레이블을 가졌다. 2016년 기준으로, 매스매티카는 100,000개의 프로그램으로 가장 인기 있는 선택이었고, 그 다음으로 50,000개의 PARI/GP 프로그램, 35,000개의 메이플 프로그램, 45,000개의 다른 언어로 작성된 프로그램이었다.^[20]

3. 11. 상호 참조 (Crossrefs)

다음은 온라인 정수열 사전(OEIS)의 주요 섹션 중 하나인 "CROSSREFS" (상호 참조)에 대한 설명이다.

Cf. 부분: 게시자가 관련성이 깊다고 인정한 수열들을 나열한다.
Adjacent sequences: 부분: ID (식별 번호)가 가까운 수열들을 보여준다.
Sequence in context: 부분: 사전식 순서에 따라 해당 수열의 앞뒤에 위치하는 수열들을 나열한다. OEIS에서의 순서는 기본적으로 부호 및 앞부분의 0, 1, -1 등은 무시하고 정렬된다.

3. 12. 키워드 (Keyword)

OEIS에는 각 수열을 특징짓는 주로 4글자로 된 표준 키워드 집합이 있다.^[23]

'''base''' - 계산 결과가 특정 위치 표기법에 따라 달라진다. 예를 들어 2, 3, 5, 7, 11, 101, 131, 151, 181 ...는 기본과 관계없이 소수이지만, 특히 10진법에서는 회문 소수이다. 대부분은 이진법에서는 회문이 아니다.
'''cofr''' - 수열은 ''e'' 또는 π의 연분수 전개를 나타낸다.
'''cons''' - 수열은 ''e'' 또는 π와 같은 수학 상수의 소수점 전개이다.
'''core''' - 소수, 피보나치 수열 등과 같이 수학 분야에 근본적인 중요성을 갖는 수열이다.
'''dead''' - 논문이나 책에 나타난 오류 수열 또는 기존 수열의 중복에 사용된다. 예를 들어 는 과 동일하다.
'''easy''' - 수열의 항을 쉽게 계산할 수 있다. 이 키워드를 가장 받을 만한 수열은 1, 2, 3, 4, 5, 6, 7, ... 이며, 각 항은 이전 항보다 1 크다.
'''fini''' - 수열은 유한하지만 표시할 수 있는 것보다 더 많은 항을 포함할 수 있다. 예를 들어 의 수열 필드는 모든 항의 약 1/4만 표시하지만, 마지막 항은 3888이라고 주석에 나와 있다.
'''frac''' - 유리수를 나타내는 분수 수열의 분자 또는 분모 수열이다. 이 키워드가 있는 모든 수열은 분자 또는 분모의 일치하는 수열에 교차 참조되어야 한다.
'''full''' - 수열 필드는 전체 수열을 표시한다. 수열에 "full" 키워드가 있으면 "fini" 키워드도 있어야 한다.
'''hard''' - 수열의 항은 쉽게 계산할 수 없다. 이 키워드는 해결되지 않은 문제에 해당하는 수열에 가장 자주 사용된다.
'''less''' - "덜 흥미로운 수열"이다.
'''more''' - 수열에 대한 더 많은 항이 필요하다.
'''mult''' - 수열은 곱셈 함수에 해당한다. 항 ''a''(1)은 1이어야 하며, ''m''과 ''n''이 상호 소수인 경우 ''a''(''mn'') 항은 ''a''(''m'')에 ''a''(''n'')을 곱하여 계산할 수 있다.
'''new''' - 지난 몇 주 동안 추가된 수열 또는 최근에 주요 확장을 한 수열이다.
'''nice''' - "예외적으로 멋진 수열"이다.
'''nonn''' - 수열은 음이 아닌 정수로 구성된다(0을 포함할 수 있음).
'''obsc''' - 수열은 모호하다고 간주되며 더 나은 정의가 필요하다.
'''sign''' - 수열 값의 일부(또는 전부)가 음수이다.
'''tabl''' - 삼각형 또는 사각형과 같은 숫자 배열을 행별로 읽어 얻은 수열이다. 전형적인 예는 행별로 읽은 파스칼의 삼각형이다.
'''unkn''' - 수열에 대해 알려진 것이 거의 없으며, 생성 공식조차 알지 못한다.
'''word''' - 특정 언어의 단어에 따라 달라진다. 예를 들어 4, 3, 3, 5, 4, 4, 3, 5, 5, 4, 3, 6, 6, 8, 8, 7, 7, 9, 8, 8 ...는 "''n''의 영어 이름에서 공백과 하이픈을 제외한 글자 수"이다.

몇몇 키워드는 상호 배타적이다. 즉, core 및 dumb, easy 및 hard, full 및 more, less 및 nice, nonn 및 sign이다.

4. 키워드 상세 설명

OEIS는 각 수열의 특징을 나타내는 약 4글자 길이의 키워드를 사용한다.^[37]^[38]^[39]

키워드	의미	설명
allocated	할당됨	투고자를 위해 할당된 수열로, 편집 중이거나 승인 대기 중이다.
allocating	할당 중	할당 과정에 있을 때 이 키워드가 붙을 수 있다.
base	기수 의존	수열의 정의가 특정 기수에 의존한다. 예를 들어 회문 소수(A002385)는 10진법에서 회문이 되는 소수이다.
bref	짧음	수열의 알려진 항이 매우 적거나, 다음 항이 매우 커서 3개 이하의 항만 표시된다.
changed	변경됨	최근에 편집되었다.
cofr	연분수	어떤 수의 연분수 전개로 얻어지는 수열이다. 예를 들어 네이피어 수(A003417)나 원주율(A001203)의 연분수 전개가 있다.
cons	상수	네이피어 수(A001113)나 원주율(A001203) 등 수학 상수의 각 자릿수를 나열한 수열이다.
core	핵심	소수(A000040)나 피보나치 수열(A000045)처럼 수학적으로 중요한 수열이다.
dead	삭제됨	중복 등록, 문헌 오류 등을 포함하지만 삭제되지 않은 수열에 붙는다. 예를 들어 메르센 소수(A000668)에 대한 A088552 등이 있다.
dumb	중요하지 않음	중요하지 않다고 판단되는 수열에 붙는다. 현재는 거의 사용되지 않는다.
easy	쉬움	수열의 각 항을 쉽게 계산할 수 있다.
eigen	고유 수열	어떤 변환을 해도 변하지 않는 수열이다. 슬론은 어떤 수열의 변환에 의해 불변인 수열을 고유 수열이라고 했다.^[40]
fini	유한	수열이 유한하다.
frac	분수	분수열의 분자 또는 분모만 가져온 수열이다.
full	완전	수열이 유한하고, 표시된 항이 전부이다.
hard	어려움	알려진 항이 적고, 다음 항을 구하기 어렵다. 메르센 소수(A000668) 등 미해결 문제와 관련된 경우가 많다.
hear	들을 만함	수치를 음정으로 변환하면 청각적으로 흥미로운 수열이다.
less	덜 중요함	재미없다고 생각되는 수열이다.
look	볼 만함	수열을 그래프로 그리면 시각적으로 흥미로운 배열이 된다.
more	더 필요함	더 많은 항이 필요하다.
mult	곱셈적	수열이 곱셈적이다. a(1) = 1이고, 서로 소인 m, n에 대해 a(mn) = a(m)a(n)을 만족한다.
new	신규	최근에 새로 투고되거나 수정되었다.
nice	흥미로움	흥미로운 수열에 붙는다.
nonn	음이 아닌 정수	수열이 음이 아닌 정수로만 구성된다.
obsc	불분명함	정의가 불분명하거나 이해하기 어렵다.
probation	가등록	가등록 상태이며, 나중에 삭제될 수 있다.
recycled	재활용됨	제안된 등록이 기각되고, 새로운 수열이 등록되었다.
sign	부호 있음	수열이 음수를 포함한다.
tabf	불규칙 배열	불규칙하지만 흥미로운 형태로 배열된 수에서 얻어진다.
tabl	삼각형 배열	파스칼의 삼각형(A007318)처럼 삼각형 형태로 배열된 수에서 얻어진 수열이다.
uned	미확인	수치나 내용에 오류가 있을 수 있다.
unkn	미지	수열의 정의나 유래를 거의 알 수 없다.
walk	한붓 그리기	한붓 그리기 등 경로에 관한 수열이다.
word	단어 의존	특정 언어에 의존하는 수열이다. 예를 들어 A005589는 영어로 zero, one, two, ... 의 글자 수이다.

몇몇 키워드는 서로 배타적이다. 예를 들어 core와 dumb, easy와 hard는 동시에 붙을 수 없다.

5. 정수가 아닌 수

OEIS는 분수, 초월수의 숫자, 복소수 등의 수열을 정수열로 변환하여 목록화한다.

분수 수열은 분자 수열과 분모 수열의 두 수열('frac' 키워드로 명명됨)로 표시된다. 예를 들어, 다섯 번째 페리 수열 $\textstyle {1 \over 5}, {1 \over 4}, {1 \over 3}, {2 \over 5}, {1 \over 2}, {3 \over 5}, {2 \over 3}, {3 \over 4}, {4 \over 5}$ 는 분자 수열 1, 1, 1, 2, 1, 3, 2, 3, 4 (A006842)와 분모 수열 5, 4, 3, 5, 2, 5, 3, 4, 5 (A006843)로 목록화된다.

π = 3.1415926535897...와 같은 중요한 무리수는 십진법 전개(여기서는 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, 9, 3, 2, 3, 8, 4, 6, 2, 6, 4, 3, 3, 8, 3, 2, 7, 9, 5, 0, 2, 8, 8, ... (A000796)), 이진법 전개(여기서는 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, ... (A004601)), 또는 연분수 전개(여기서는 3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, ... (A001203))와 같은 대표적인 정수열로 목록화된다.

0은 때때로 "존재하지 않음"을 나타내기 위해 사용된다. 예를 들어, A104157의 n번째 항은 "가능한 한 작은 n × n개의 연속된 소수를 사용하여 마방진을 만들 때, 그 최소의 소수"이다. a(1)은 2이다. a(3)을 구하는 것은 다소 어렵지만 1480028129이다^[35]。 n = 2일 때는 그러한 마방진이 존재하지 않으므로, a(2)는 0으로 되어 있다.

0이 본래의 의미를 가지는 수열에서는, 이 용법으로 -1이 대신 사용되기도 한다. 예를 들어 A072041 등이 있다.

OEIS에서는 정수가 주역이지만, 어떤 방법으로든 정수열로 변환함으로써 정수가 아닌 수도 다루어진다고 할 수 있다.

유리수의 열은 분자의 열과 분모의 열이라는 두 개의 정수열로 간주할 수 있다. 예를 들어, 파레이 수열 0/1, 1/1, 0/1, 1/2, 1/1, 0/1, 1/3, 1/2, 2/3, 1/1, …에 대해서는, 그 분자의 열 0, 1, 0, 1, 1, 0, 1, 1, 2, 1, … (A006842) 과 분모의 열 1, 1, 1, 2, 1, 1, 3, 2, 3, 1, … (A006843)이 데이터베이스에 수록되어 있다.

원주율 = 3.1415926535897… 은 초월수이지만, 각 자릿수를 나열하여 만들 수 있는 정수열 3, 1, 4, 1, 5, 9, 2, 6, … (A000796)이나, 연분수 전개하여 만들 수 있는 정수열 3, 7, 15, 1, 292, 1, … (

6. 자기 참조 수열

OEIS 초창기에 OEIS 자체의 수열 번호를 사용하여 정의된 수열들이 제안되었다. 슬론은 "이러한 수열들을 오랫동안 추가하는 것을 꺼렸는데, 부분적으로는 데이터베이스의 위엄을 유지하고 싶었고, 부분적으로는 A22가 11개 항까지만 알려져 있었기 때문입니다!"라고 회상했다.^[19]

슬론이 OEIS에 받아들인 가장 초기의 자기 참조 수열 중 하나는 ''a''(''n'') = 수열 A_''n''의 ''n''번째 항 또는 A_''n''이 ''n''개 미만의 항을 가지면 –1 이다.

A100544는 수열 A_''n''에 주어진 첫 번째 항을 나열하지만, 오프셋에 대한 의견이 바뀌면서 때때로 업데이트해야 한다.

이러한 사고방식은 "수열 A_''n''은 숫자 ''n''을 포함하는가?"라는 질문으로 이어지며, A053873인 "OEIS 수열 A_''n''이 ''n''을 포함하는 숫자 ''n''"과 A053169인 "''n''은 수열 A_''n''에 만약 그리고 오직 그 경우에만 ''n''이 수열 A_''n''에 없는 경우에만 이 수열에 있습니다"와 같은 수열을 낳았다.

53873이 A053873의 구성원인지 여부를 결정할 수 없다.
53169가 A053169의 구성원이면서 동시에 아님을 증명할 수 있다. 이것은 러셀의 역설의 한 형태이다.

7. 슬론의 간극 (Sloane's Gap)

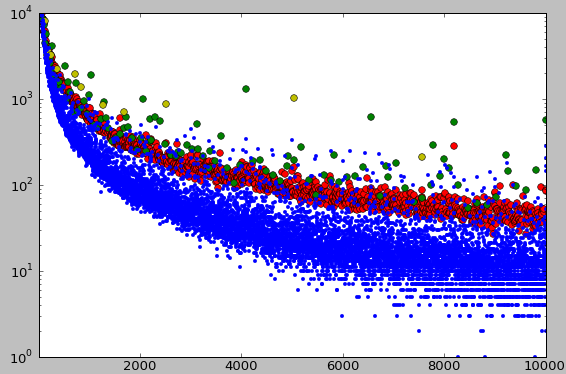
슬론의 간극 플롯: OEIS 데이터베이스에서 각 정수(x축)의 발생 횟수(y축 로그 스케일)

2009년, OEIS 데이터베이스는 필립 구글리에메티에 의해 각 정수의 "중요도"를 측정하는 데 사용되었다.^[25] 오른쪽 그림은 두 개의 뚜렷한 점군 사이에 명확한 "간극"을 보여준다.^[26] 이 간극은 "흥미롭지 않은 수"(파란색 점)와 OEIS의 수열에서 비교적 더 자주 나타나는 "흥미로운" 수 사이에 존재한다. "흥미로운 수"에는 소수(빨간색), ''a''^''n'' 형태의 수(녹색), 고도로 합성된 수(노란색)가 포함된다.

이러한 현상은 니콜라 가브리트, 장-폴 들라에, 엑토르 제닐에 의해 연구되었다. 이들은 알고리즘 복잡성의 관점에서 두 점군의 속도를 설명했고, 소수, 짝수, 기하학적 수열, 피보나치 수와 같은 수열에 대한 인공적인 선호도를 바탕으로 사회적 요인에 의해 간극을 설명했다.^[27] 슬론의 간극은 2013년 넘버파일 비디오에 소개되었다.^[28]

8. 추가 참고 도서 목록

N. J. A. 슬론, "My favorite integer sequences", C. Ding, T. Helleseth, H. Niederreiter (eds.), ''Sequences and their Applications (Proceedings of SETA '98)''. London: Springer-Verlag, 1999, pp. 103–130. My favorite integer sequences^영어
N. J. A. 슬론, "The On-Line Encyclopedia of Integer Sequences", ''Notices of the American Mathematical Society'', vol. 50, no. 8, 2003, pp. 912–915. The On-Line Encyclopedia of Integer Sequences^영어
N. J. A. 슬론, S. 플루프, ''The Encyclopedia of Integer Sequences''. San Diego: Academic Press, 1995. ISBN 0-12-558630-2. The Encyclopedia of Integer Sequences^영어
사라 C. 빌리, 브리짓 E. 테너, "Fingerprint databases for theorems", ''Notices of the American Mathematical Society'', vol. 60, no. 8, 2013, pp. 1034–1039. Fingerprint databases for theorems^영어

참조

_[1] 웹사이트 Goals of The OEIS Foundation Inc. http://oeisf.org/ind[...] 2017-11-06
_[2] 문서 Registration is required for editing entries or submitting new entries to the database
_[3] 웹사이트 The OEIS End-User License Agreement - OeisWiki https://oeis.org/wik[...] 2023-02-26
_[4] 웹사이트 Transfer of IP in OEIS to the OEIS Foundation Inc. http://oeisf.org/ind[...] 2010-06-01
_[5] 웹사이트 The On-Line Encyclopedia of Integer Sequences (OEIS) https://oeis.org
_[6] 웹사이트 FAQ for the On-Line Encyclopedia of Integer Sequences https://oeis.org/FAQ[...] OEIS Foundation 2024-06-22
_[7] 웹사이트 The Email Servers and Superseeker https://oeis.org/ol.[...] 2024
_[8] 서적 Analytic Number Theory, Modular Forms and q-Hypergeometric Series Springer International Publishing
_[9] 뉴스 In a 'random world,' he collects patterns https://www.nytimes.[...] 1987-01-27
_[10] 간행물 Journal of Integer Sequences http://www.cs.uwater[...]
_[11] 백과사전 Editorial Board http://oeis.org/wiki[...]
_[12] 웹사이트 New version of OEIS http://oeisf.org/ann[...] 2011-01-21
_[13] 웹사이트 '[seqfan] A200000' http://list.seqfan.e[...] 2011-11-14
_[14] 웹사이트 '[seqfan] A200000 chosen' http://list.seqfan.e[...] 2011-11-22
_[15] 웹사이트 Suggested Projects http://oeis.org/wiki[...] 2011-11-22
_[16] 웹사이트 Fifty Years of Integer Sequences https://www.mathvalu[...] 2023-12-04
_[17] 학술지 "A Handbook of Integer Sequences" Fifty Years Later 2023
_[18] 웹사이트 Welcome: Arrangement of the Sequences in Database https://oeis.org/wik[...] 2016-05-05
_[19] 웹사이트 My favorite integer sequences http://neilsloane.co[...]
_[20] 웹사이트 Explanation of Terms Used in Reply From https://oeis.org/eis[...] OEIS
_[21] 웹사이트 OEIS Style sheet http://oeis.org/wiki[...]
_[22] 웹사이트 B-Files http://oeis.org/wiki[...]
_[23] 백과사전 Explanation of Terms Used in Reply From http://oeis.org/clas[...]
_[24] 문서 The person who submitted A085808 did so as an example of a sequence that should not have been included in the OEIS. Sloane added it anyway, surmising that the sequence "might appear one day on a quiz."
_[25] 웹사이트 Chasse aux nombres acratopèges http://www.drgoulu.c[...] 2008-08-24
_[26] 웹사이트 La minéralisation des nombres http://www.drgoulu.c[...] 2016-12-25
_[27] 학술지 Sloane's Gap. Mathematical and Social Factors Explain the Distribution of Numbers in the OEIS https://scholarship.[...] 2011
_[28] Youtube Sloane's Gap https://www.youtube.[...] 2013-10-15
_[29] 문서 サイトトップページ最下部の表記より "Last modified March 29 22:32 EDT 2018. Contains 301549 sequences."
_[30] 문서 Welcome - Copyright Notice]の項目より "This database and its associated files are copyright 2011 by The OEIS Foundation Inc." 最終アクセス 2012年1月4日
_[31] 문서 Recent Additions] のページで最新の追加項目を見る事が出来る。最終アクセス 2012年1月4日
_[32] 문서 Journal of Integer Sequences] 論文を無料でダウンロード可能
_[33] 문서 OEIS: Brief history]
_[34] 문서 Transfer of IP in OEIS to The OEIS Foundation Inc.]
_[35] 문서 Harvey Heinz, Minimum Consecutive Primes -3] この場合の最小の魔方陣
_[36] MathWorld Circle Division by Lines
_[37] 웹사이트 OEIS で用いられるキーワードの一覧 https://oeis.org/eis[...]
_[38] OeisWiki Clear-cut examples of keywords https://oeis.org/wik[...]
_[39] Charles R Greathouse IV Keywords https://oeis.org/wik[...]
_[40] 논문 Some canonical sequences of integers http://www.research.[...] 1995
_[41] MathWorld Rule 110
_[42] 웹사이트 OEIS における著者の表示のルール http://oeis.org/clas[...]
_[43] 웹인용 Goals of The OEIS Foundation Inc. http://oeisf.org/ind[...] 2017-11-06
_[44] 문서 등록은 수열을 편집하거나, 데이터베이스에 새로운 수열을 보내는 데 필요하다.

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com